時系列データにおける異常検知
時系列データにおける異常検知
はじめに
カブクで機械学習エンジニアをしている大串正矢です。今回は時系列データにおける異常検知について書きます。
背景
時系列データの異常検知の手法は多種多様に存在していますがウェブ上にまとまった情報が日本語でないため記述することにしました。以前に記述した異常検知の基礎に異常検知の基礎的な内容が記述されているのでその内容を踏まえた上で読んで頂けると理解がしやすいと思います。
時系列データにおける異常検知手法
通常の異常検知手法との違いは時系列データなのでデータが独立ではなくデータ間に依存性が存在することです。前回紹介した手法はデータが独立であることを仮定しているため使用できません。
異なる手法が必要になります。
代表的な手法を下記に記述します。
- 動的時間伸縮法
- 利点:シンプル
- 欠点:ノイズに弱い
- 特異スペクトル変換
- 利点:ノイズに頑健
- 欠点:計算コストが高い
- 自己回帰モデル
- 利点:周期性があるデータに強い。異常検知以外にも時系列予測、変化点検知に使用可能
- 欠点:次数が決めうちのため状態が一定なものでないと適用が難しい
- 状態空間モデル
- 利点:状態が変化しても対応可能かつノイズに強い。自己回帰モデルと同様に時系列予測、変化点検知に使用可能
- 欠点:周期性があり安定しているデータには対応しづらい
下記の点から今回は自己回帰モデルと状態空間モデルにフォーカスして記述します。
- 自己回帰モデルによる異常検知は予測モデルを自己回帰モデルから他のモデルに置き換えても使用可能なため拡張性が高い
- 状態空間モデルは内部状態が変化しても対応可能なため、状態が変化する機器の異常検知にも対応可能。例:車のセンサーなど
自己回帰モデル
- モデルの推定
- モデルを定義し、正常なデータから学習
- 異常度の定義
- 実波形と予測波形の差
- 閾値の設定
- 検証データで設定もしくは異常検知の基礎の閾値設定の部分で紹介した分位点やカイ2乗分布を用いる
データについて
下記の図のようにデータをwindowで区切って扱います。このようにすることで行列としてデータを扱うことができ、行列計算などの処理が容易になります。ここで区切った各ウィンドウをεと置きます。
適切なwindowの幅を設定してデータを分割します。適切なwindowの幅はAICと呼ばれる手法で決めれますがこの点は後述します。
自己回帰モデルの学習
下記に簡単な図を示します。学習用の波形と予測用の波形を用意しています。この予測波形をうまく模倣できるように自己回帰モデルを推定します。
この時のwindowの幅が次数rになります。
\begin{align}
y^{t} \equiv \epsilon^{(t+r)}
\end{align}
\begin{align}
\boldsymbol{x}^{t} \equiv \left( \begin{array}{c} \epsilon^{(t)} \ \epsilon^{(t+1)}
\ \vdots \ \epsilon^{(t+r-1)} \end{array} \right)
\end{align}
\begin{align}
N \equiv T – r
\end{align}
\begin{align}
y^{t} \approx \alpha_1\epsilon^{(t-r)} + \alpha_2\epsilon^{(t-r+1)} + … + \alpha_{r-1}\epsilon^{(t-2)} + \alpha_{r}\epsilon^{(t-1)}
\end{align}
このモデルの予測値と実測値の予測誤差を正規分布でモデル化します。
\begin{align}
p(y^{n} | \boldsymbol{\alpha}, \sigma) = \mathcal{N}(y^{n} | \boldsymbol{\alpha}^T\boldsymbol{x}, \sigma^2)
\end{align}
上式の平均を下記で置き換え
\begin{align}
\mu=\boldsymbol{\alpha}^{T}\boldsymbol{x}^{(n)}
\end{align}
出力値を下記で置き換え
\begin{align}
x’=y^{n}
\end{align}
この正規分布に対して対数尤度関数の式を立てます。下記の式は正規分布で使用した対数尤度です。
\begin{align}
\frac{1}{2\sigma^2}(x’ – \mu)^2 + \frac{1}{2}\ln(2\pi\sigma^2)
\end{align}
ここで元の時系列データを下記のように変更します。
\begin{align}
D = {(\boldsymbol{x}^{(1)}, y^{(1)}), …, (\boldsymbol{x}^{(N)}, y^{(N)}) }
\end{align}
N個分のデータを考慮する必要があるので予測誤差は下記の式になります。
\begin{align}
L(\boldsymbol{\alpha}, \sigma^2 | D) = -\frac{N}{2}\ln(2\pi\sigma^2) – \frac{1}{2\sigma^2}\sum^N_{n=1}[y^{n} – \boldsymbol{\alpha}^T\boldsymbol{x}^{(n)}]^{2}
\end{align}
ではこの予測誤差の分布が最小になれば予測と実測の値が最小になるので最小な値を取れるようなαとσを導出します。
αで微分して0と等価とすると
\begin{align}
0 = -\frac{1}{2\sigma^2}(-\boldsymbol{X}\boldsymbol{y} + \alpha \boldsymbol{X}\boldsymbol{X}^T)
\end{align}
\begin{align}
\boldsymbol{\alpha} = [\boldsymbol{X}\boldsymbol{X}^T]^{-1}\boldsymbol{X}\boldsymbol{y}
\end{align}
σで微分して0と等価とすると
\begin{align}
0 = -\frac{N4\pi\sigma}{4\pi\sigma^2} + \frac{2}{2\sigma^{3}}\sum^N_{n=1}[y^{n} – \boldsymbol{\alpha}^T\boldsymbol{x}^{(n)}]^{2}
\end{align}
\begin{align}
\sigma = \frac{1}{N}\sum^N_{n=1}[y^{n} – \boldsymbol{\alpha}^T\boldsymbol{x}^{(n)}]^{2}
\end{align}
次数rの決定
モデルの複雑性がハイパーパラメータである次数rで定まります。クロスバリデーションなどの手法でrを決めるのは時間的な順序があるため使えないのでこの複雑さを決める基準としてAIC(赤池情報量基準)を用います。
\begin{align}
\ln|\sigma| + \frac{2r}{N}
\end{align}
上記の数式が最小になるようにモデルを選択します。
Pythonによる実装
自己回帰モデルを実装します
今回は統計的なモデルが利用できるライブラリである”StatsModels”を使用してモデルを実現します。
データはオーストラリアの公開されている気温のデータを使用しました。ただしデータの中に?などが混じっており数値データ以外の項目があるので適宜削除してください。
#!/usr/bin/env python3
import pylab
from statsmodels.tsa.ar_model import AR
import numpy as np
from pandas import Series
# Reference
# data : https://raw.githubusercontent.com/vincentarelbundock/Rdatasets/master/csv/texmex/nidd.csv # noqa
def train_autoregression(train_data, test_data):
# train autoregression
print(train_data)
model = AR(train_data)
model_fit = model.fit()
window = model_fit.k_ar
coef = model_fit.params
print('Lag: %s' % model_fit.k_ar)
print('Coefficients: %s' % model_fit.params)
# make predictions
print('aic {}'.format(model_fit.aic))
history = train_data[len(train_data) - window:]
history = [h for h in history]
predictions = []
for index, test in enumerate(test_data):
length = len(history)
lag = [history[i] for i in range(length - window, length)]
yhat = coef[0]
for d in range(window):
yhat += coef[d+1] * lag[window - d - 1]
obs = test
predictions.append(yhat)
history.append(obs)
return predictions
def main():
wave_data = Series.from_csv('../data/raw/daily-minimum-temperatures-in-me.csv', header=0) # noqa
X = np.array(wave_data.values, dtype=float)
print(len(X))
train_data_size = 3000
train_data, test_data = X[1:train_data_size], X[train_data_size:]
predict = train_autoregression(train_data, test_data)
pylab.figure(figsize=(14, 8))
pylab.subplot(211)
pylab.xlabel('time')
pylab.ylabel('temperature')
pylab.plot(test_data, label='real')
pylab.plot(predict, '--', label='predict')
pylab.legend(loc='upper right')
pylab.show()
if __name__ == '__main__':
main()
コードの下記の部分で自己回帰モデルの出力を実現しています。
for d in range(window):
yhat += coef[d+1] * lag[window - d - 1]
StatsModelsのライブラリがAICに基づく最適な次数を設定してくれています。
オレンジが予測波形、青が実波形で波形を模倣できていることが確認できます。
異常度の計算
ホテリング理論を用いて下記のように定義します。
\begin{align}
a(\epsilon^{(t)}) = \frac{1}{\sigma^2}[\epsilon^{(t)} - \sum^r_{l=1}{\alpha_{l}\epsilon^{(t-l)}}]^{2}
\end{align}
の部分は自己回帰モデルで導出した値ですが、この部分は他の予測モデルで置き換え可能です。
閾値の設定
前回の手法と同様に閾値は学習データの分位点を基準にするかもしくは自由度1のカイ2乗分布を当てはめて導出します。
ここで異常度は各点において計算されるので異常と判定する場合に何度、閾値を超えたかも設定する必要があります。
その代わり各点における異常度が計算できているため変化点の検知も可能になっています。
自己回帰モデルの派生
詳細は記述しませんが今回紹介したモデルの派生系として下記のようなモデルがあります。
- MAモデル(移動平均モデル)
- ARMAモデル(自己回帰移動平均モデル)
- ARIMAモデル(自己回帰和文移動平均モデル)
- SARIMAモデル(季節自己回帰和文移動平均モデル)
異常度の導出、閾値の導出は自己回帰モデルと同様なため最初に拡張性が高いと記述したのはそのためです。
状態空間モデル
定常的な時系列データを扱うのに便利な自己回帰モデルを紹介しました。ここからは状態が変化する時系列を扱える状態空間モデルについて紹介します
イメージを掴みやすい動画を見つけたのでこちらをまず紹介します。
見えない状態空間の影響を受けてなおかつそれが時系列データの場合に有効な手法になります。正常な状態だが微妙に状態が変化する事象は現実的な問題として多数存在します。そのようなケースにおいて有効です。
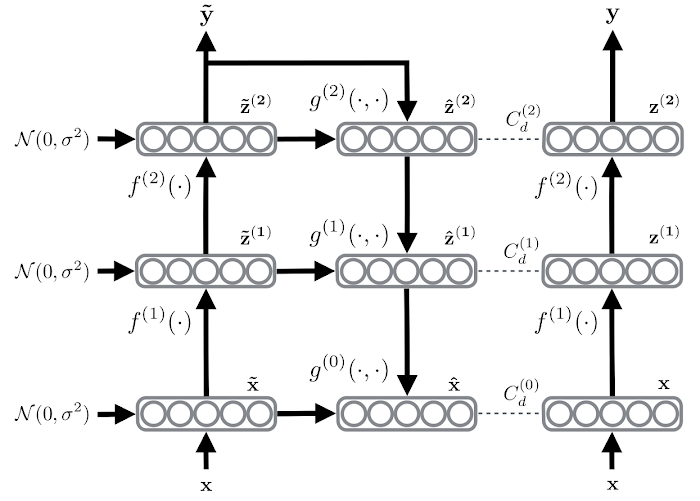
上記の図のように状態空間と観測空間に分けます。このようなモデルを状態空間モデルと呼びます。
下記の数式で記述できます。
\begin{align}
p(\boldsymbol{x}^{t}|\boldsymbol{z}^{t}) = \mathcal{N}(\boldsymbol{x}^{t}| \boldsymbol{C}\boldsymbol{z}^{t}, \boldsymbol{R})
\end{align}
\begin{align}
p(\boldsymbol{z}^{t}|\boldsymbol{z}^{t-1}) = \mathcal{N}(\boldsymbol{z}^{t}| \boldsymbol{A}\boldsymbol{z}^{t - 1}, \boldsymbol{Q})
\end{align}
- A:観測空間を表現する行列
- C:状態空間を表現する行列
- R:観測のばらつき
- Q:内部状態のばらつき
本記事ではこれらの未知のパラメータの導出には言及しません。入門 機械学習による異常検知―Rによる実践ガイド-井手-剛のp.214からp.220に導出があります。
状態空間モデル
観測されたデータから状態変数の確率分布を求めます。
\begin{align}
p(\boldsymbol{z}^{t}|\boldsymbol X_t) = \mathcal{N}(\boldsymbol{z}^{t}| \boldsymbol{\mu}_{t}, \boldsymbol V_t)
\end{align}
下記の結果用います。本記事ではこれらの未知のパラメータの導出には言及しません。入門 機械学習による異常検知―Rによる実践ガイド-井手-剛のp.221からp.224に導出があります。
t=0の時の状態変数の平均を
\begin{align}
\boldsymbol{A} \boldsymbol \mu_{0} = \boldsymbol z_{0}
\end{align}
として定義し、t=1,...Tに対して次の計算を繰り返します。
\begin{align}
\boldsymbol K_t = \boldsymbol Q_{t-1}\boldsymbol{C}^{T}(\boldsymbol{R} + \boldsymbol{C}\boldsymbol Q_{t-1}\boldsymbol{C}^T)^{-1}
\end{align}
\begin{align}
\boldsymbol \mu_t = \boldsymbol{A}\mu_{t-1}+ \boldsymbol K_{t}(\boldsymbol{x}^{(t)} - \boldsymbol{C}\boldsymbol{A}\mu_{t-1})
\end{align}
\begin{align}
\boldsymbol V_t = (\boldsymbol I_m - \boldsymbol K_{t}\boldsymbol{C})\boldsymbol Q_{t-1}
\end{align}
\begin{align}
\boldsymbol Q_t = \boldsymbol{Q} + \boldsymbol{A}\boldsymbol V_t\boldsymbol{A}^{T}
\end{align}
この時のKtはカルマンゲインと呼ばれ観測値とのばらつきに対する反応の敏感さを表現しています。
状態変数における平均と分散が導出できます。
ここでt-1までの観測データが与えられた時のxの分布を与えます。tの時の予測分布を考えます。多変数正規分布のベイズ公式より
\begin{align}
p(\boldsymbol{x}^{(t)} | \boldsymbol X_{t-1}) = \mathcal{N}(\boldsymbol{x}^{(t)} | \boldsymbol{C}\boldsymbol{A}\boldsymbol \mu_{t-1}, \boldsymbol{R} + \boldsymbol{C}\boldsymbol Q_{t-1}\boldsymbol{C}^{T})
\end{align}
QとAは状態変数のパラメメータなので状態変数のパラメータが影響して正規分布のモデルが変化しています。さらに平均は一つ前の平均、分散は一つ前の状態変数の分散に影響して決定しています。
下記の図のように正規分布が変化していくイメージです。
実装
状態空間モデルの実装はPyFluxというライブラリを使用します。
これによって下記に示すわずかなコードで実現が可能ですが再現しているのはローカルレベルモデルのため若干状態空間モデルと異なります。
#!/usr/bin/env python3
import numpy as np
from pandas import Series
import pyflux as pf
import matplotlib.pyplot as plt
# Reference
# data : https://raw.githubusercontent.com/vincentarelbundock/Rdatasets/master/csv/texmex/nidd.csv # noqa
def train_autoregression(train_data, test_data):
# train autoregression
print(train_data)
model = pf.LLEV(data=train_data, target='Nile')
x = model.fit()
x.summary()
model.plot_fit(figsize=(15, 10))
plt.figure(figsize=(15, 5))
for i in range(10):
model_index = np.array(model.index)
plt.plot(model_index, model.simulation_smoother(
model.latent_variables.get_z_values())[1][0:model_index.shape[0]])
plt.show()
def main():
wave_data = Series.from_csv('../data/raw/daily-minimum-temperatures-in-me.csv', header=0) # noqa
X = np.array(wave_data.values, dtype=float)
train_data_size = 3000
train_data, test_data = X[1:train_data_size], X[train_data_size:]
train_autoregression(train_data, test_data)
if __name__ == '__main__':
main()
下記に上から実データに対するモデルのフィット度合いの確認、予測されたモデルとそのモデルが95%の確率で取りうる範囲、データから観測されたノイズを確認できます。
異常スコアの計算
正規分布による異常度を計算すれば良いので下記のような式になります。
\begin{align}
a(\boldsymbol{x}^{(t)}) = (\boldsymbol{x}^{(t)} - \boldsymbol{C}\boldsymbol{A}\boldsymbol \mu_{t-1})\boldsymbol{\sigma}^-1_{t}(\boldsymbol{x}^{(t)} - \boldsymbol{C}\boldsymbol{A}\boldsymbol \mu_{t-1})
\end{align}
\begin{align}
\boldsymbol{\sigma_t} \equiv \boldsymbol{R}+\boldsymbol{C}\boldsymbol Q_{t-1}\boldsymbol{C}^{T}
\end{align}
閾値の設定
検証データで設定するか分位点による設定になります。
状態空間モデルも異常度は各点において計算されるので異常と判定する場合に何度、閾値を超えたかも設定する必要があります。
その代わり各点における異常度が計算できているため変化点の検知も可能になっています。
最後に
弊社では異常検知以外にも物体検出、3次元データ検索エンジンの開発をしています。これらに興味があるエンジニアがいらっしゃれば絶賛採用中なので是非、弊社へ応募してください。
参考
時系列解析_理論編
入門 機械学習による異常検知―Rによる実践ガイド
時系列データに対する異常検知
Autoregression Models for Time Series Forecasting With Python
Understanding Kalman Filters, Part 4: Optimal State Estimator Algorithm
Gaussian State Space Models
その他の記事
Other Articles


関連職種
Recruit